Papers
2024
-
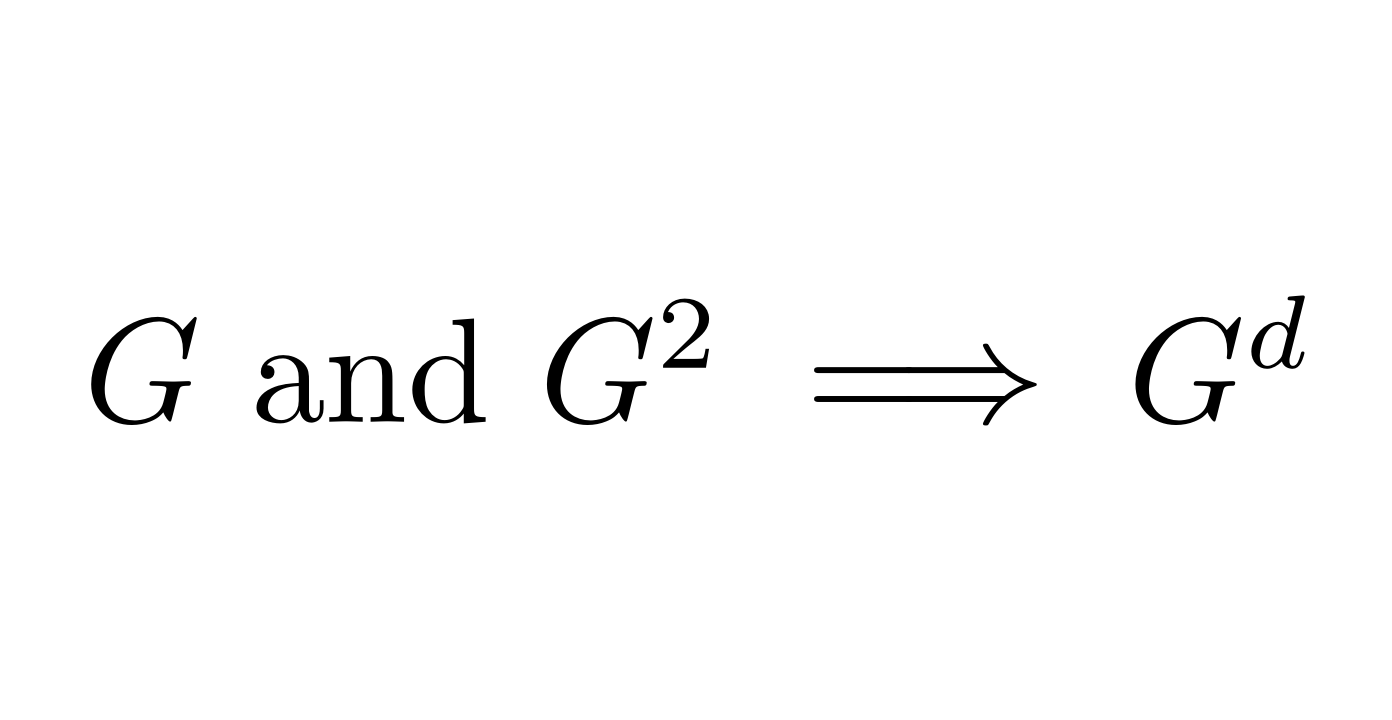Towards a Complete Local-Global PrincipleNikola KuzmanovskiSubmitted, 2024Ahlswede and Cai proved that if a simple graph has nested solutions (NS) under the edge-isoperimetric problems, and the lexicographic (lex) order produces NS for its second cartesian power, then the lex order produces NS for any finite cartesian power. Under very general assumptions, we prove that if a graph and its second cartesian power have NS, then so does any finite cartesian power. Harper asked if this is true without any restriction. We also conjecture that it is. All graphs studied in the literature for which the lex order is optimal are regular. This lead Bezrukov and Elsässer to conjecture that if the lex order is optimal for the second cartesian power, then the original graph is regular. A counterexample to this conjecture is provided.
-
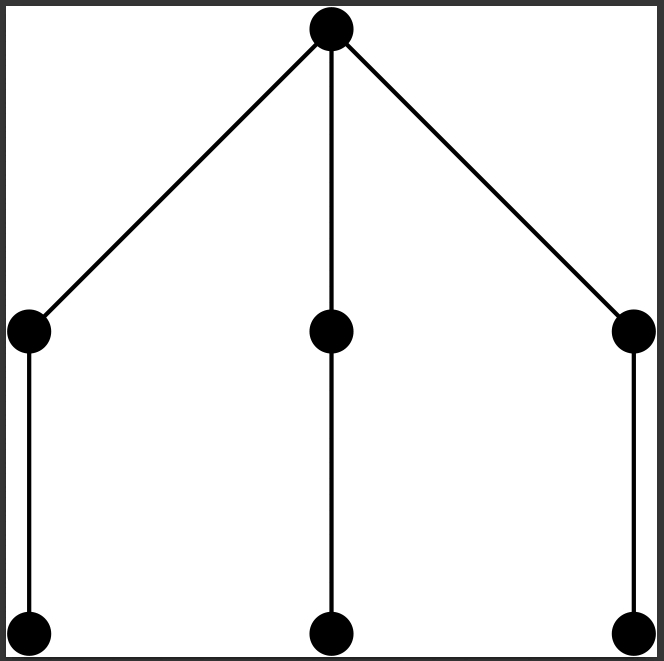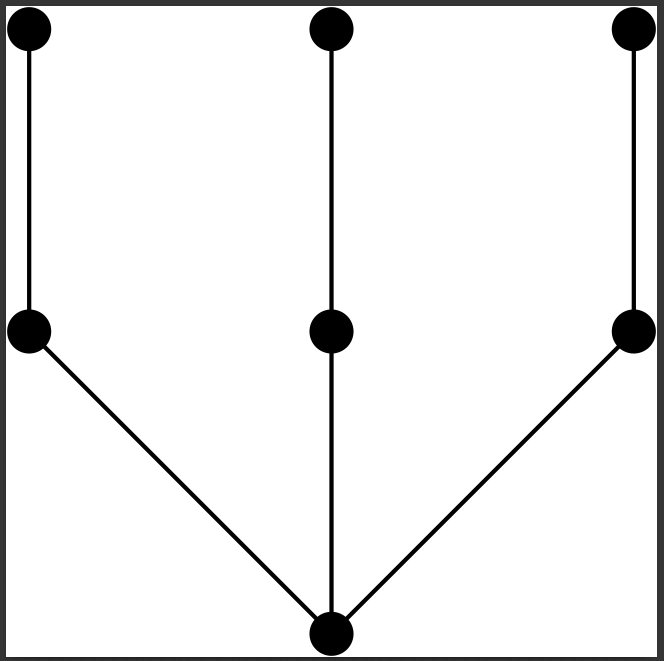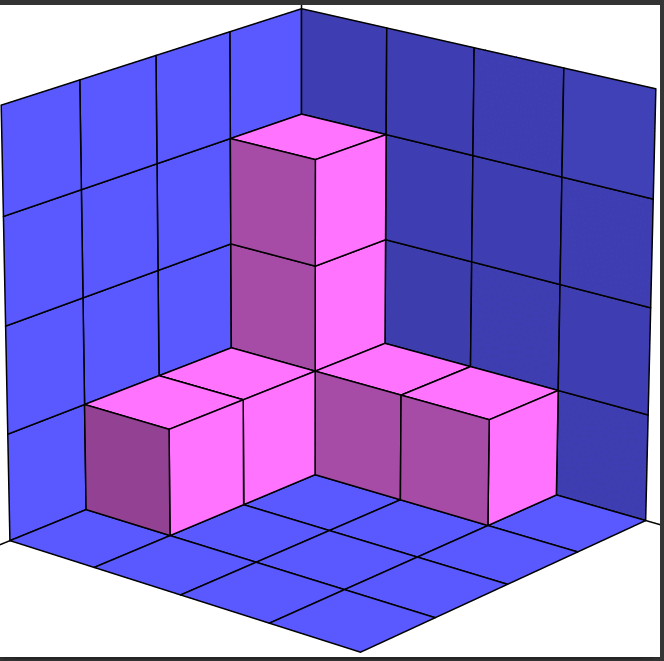
Macaulay Posets and RingsNikola KuzmanovskiSubmitted, 2024Macaulay posets are posets in which an analog of the Kruskal-Katona Theorem holds. Macaulay rings (also called Macaulay-Lex rings) are rings in which an analog of Macaulay’s Theorem for lex ideals holds. The study of both of these objects started with Macaulay almost a century ago. Since then, these two branches have developed separately over the past century, with the last link being the Clements-Lindstr¨om Theorem. For every ring that is the quotient of a polynomial ring by a homogeneous ideal we define the poset of monomials. Under certain conditions, we prove a Macaulay Correspondence Theorem, a ring is Macaulay if and only if its poset of monomials is Macaulay. Furthermore, the tensor product of rings corresponds to the Cartesian product of the posets of monomials. This allows us to transfer results between rings and posets. The Macaulay Correspondence Theorem generalizes a theorem by Shakin, and allows ideals that are not monomial with orders that are different from the lexicographic one. By using this translation, we give several answers to a problem posed by Mermin and Peeva, a positive answer to Hoefel’s question about applying Macaulay poset theory to ring theory, and deduce several other results in both algebra and extremal combinatorics. A new proof of the Mermin-Murai Theorem on colored square free rings is presented by using star posets. We extend the Mermin-Murai Theorem to rings that are not square free by using the spider Macaulay Theorem of Bezrukov and Els¨asser. Using the Mermin-Peeva and Shakin results about adding a variable to a ring such that it remains Macaulay, we give an answer to a question posed by Bezrukov and Leck about taking the product of a Macaulay poset with a chain. Some results of Chong also give answers to the Bezrukov-Leck problem. All of these results have a common feature. They involve the tensor product of rings whose Hasse graphs of the poset of monomials are trees. We call such rings, tree rings. We give a classification of Macaulay rings that are the tensor product of a tree ring. Finally, we show that there are Macaulay rings that are not the tensor product of tree rings, and present the first examples of Macaulay rings that are not quotients by a monomial ideal and not quotients by a toric ideal.
-
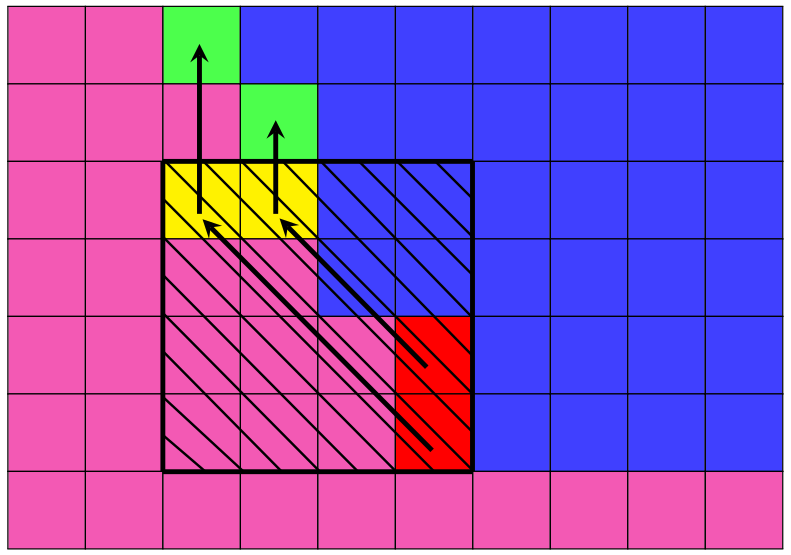Reflect-Push Methods Part I. Two Dimensional TechniquesNikola Kuzmanovski, and Jamie RadcliffeElectronic Journal of Combinatorics, 2024We determine all maximum weight downsets in the product of two chains, where the weight function is a strictly increasing function of the rank. Many discrete isoperimetric problems can be reduced to the maximum weight downset problem. Our results generalize Lindsay’s edge- isoperimetric theorem in two dimensions in several directions. They also imply and strengthen (in several directions) a result of Ahlswede and Katona concerning graphs with maximal number of adjacent pairs of edges. We find all optimal shifted graphs in the Ahlswede-Katona problem. Furthermore, the results of Ahlswede-Katona are extended to posets with a rank increasing and rank constant weight function. Our results also strengthen a special case of a recent result by Keough and Radcliffe concerning graphs with the fewest matchings. All of these results are achieved by applications of a key lemma that we call the reflect-push method. This method is geometric and combinatorial. Most of the literature on edge-isoperimetric inequalities focuses on finding a solution, and there are no general methods for finding all possible solutions. Our results give a general approach for finding all compressed solutions for the above edge-isoperimetric problems. By using the Ahlswede-Cai local-global principle, one can conclude that lexicographic so- lutions are optimal for many cases of higher dimensional isoperimetric problems. With this and our two dimensional results we can prove Lindsay’s edge-isoperimetric inequality in any dimension. Furthermore, our results show that lexicographic solutions are the unique solutions for which compression techniques can be applied in this general setting.
2023
-
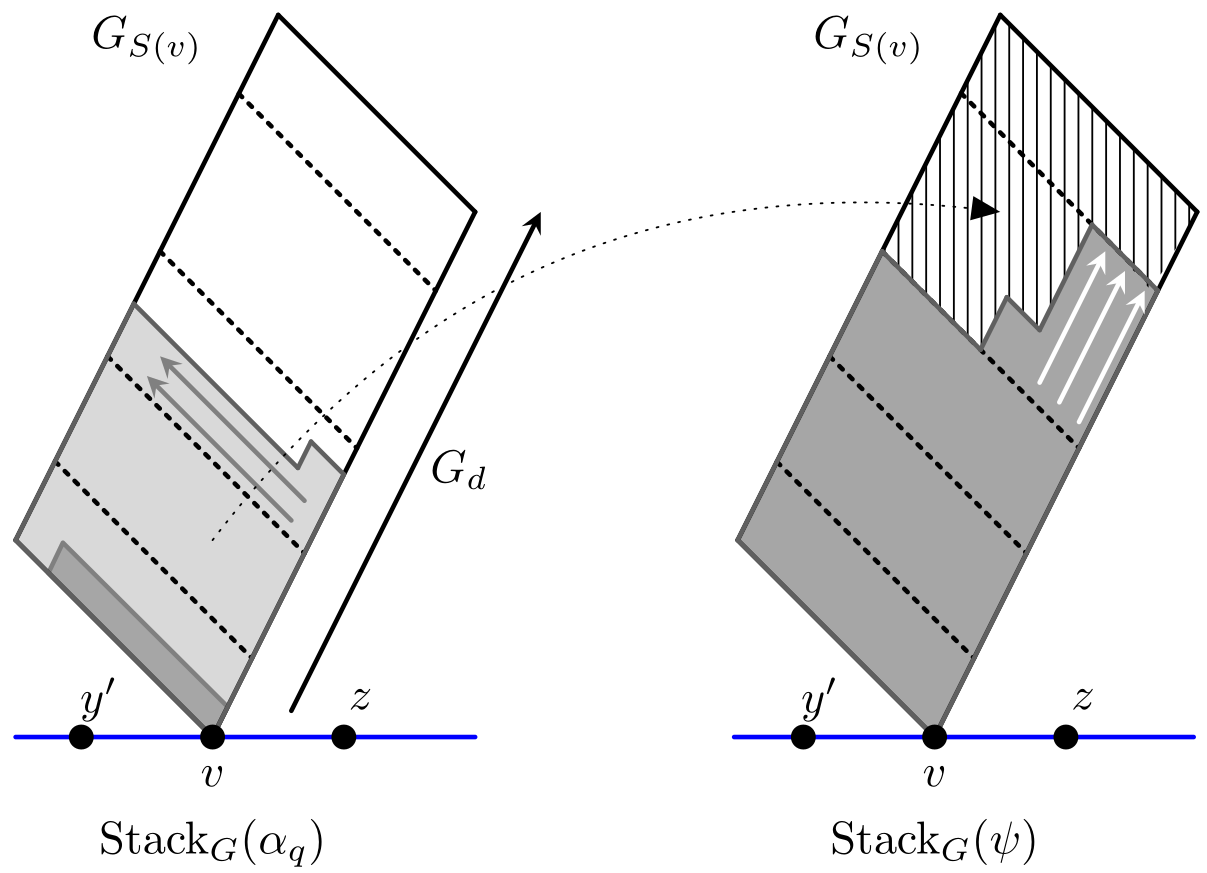Pull-Push Method. A New Approach to Edge-Isoperimetric ProblemsSergei Bezrukov, Nikola Kuzmanovski, and Jounglag LimDiscrete Mathematics, 2023We prove a generalization of the Ahlswede-Cai local-global principle. A new technique to handle edge-isoperimetric problems is introduced which we call the pull-push method. Our main result includes all previously published results in this area as special cases with the only exception of the edge-isoperimetric problem for grids. With this we partially answer a question of Harper on local-global principles. We also describe a strategy for further generalization of our results so that the case of grids would be covered, which would completely settle Harper’s question.
2018
-
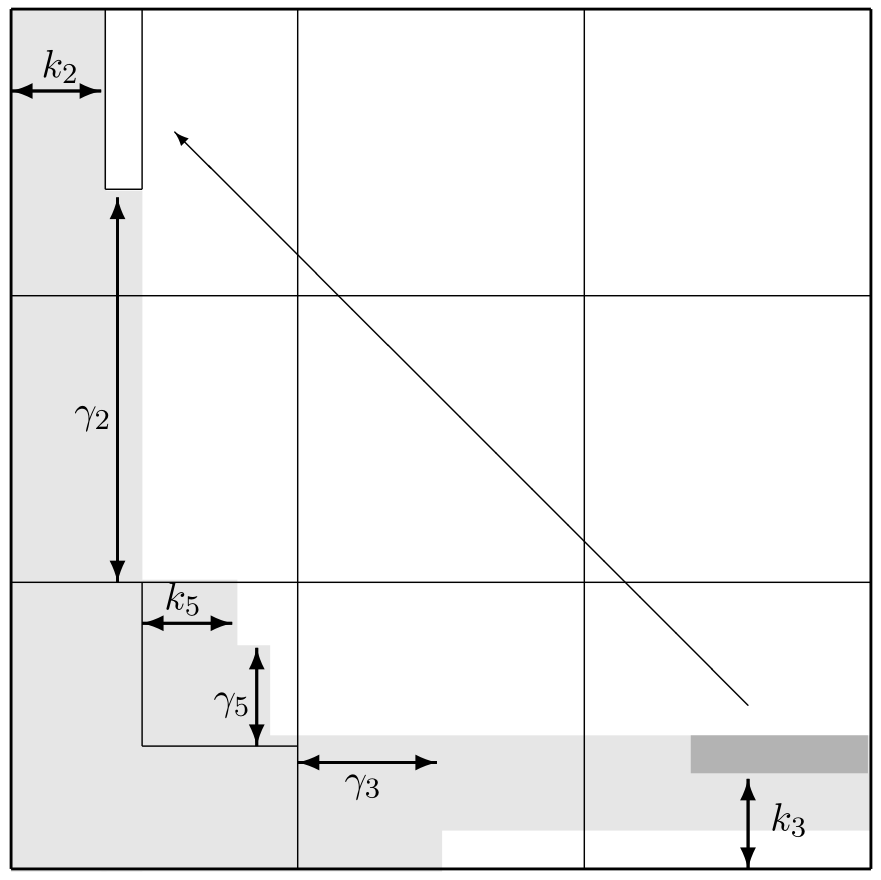New Infinite Family of Regular Edge-Isoperimetric GraphsSergei Bezrukov, Pavle Bulatovic, and Nikola KuzmanovskiTheoretical Computer Science, 2018We introduce a new infinite family of regular graphs admitting nested solutions in the edge- isoperimetric problem for all their Cartesian powers. The obtained results include as special cases most of previously known results in this area.
